优化器

定义通用的 fastai 优化器及其变体

add_docs(_BaseOptimizer, 
         all_params="List of param_groups, parameters, and hypers",
         freeze_to="Freeze parameter groups up to `n`",
         freeze="Freeze up to last parameter group",
         unfreeze="Unfreeze the entire model",
         set_hypers="`set_hyper` for all `kwargs`",
         set_hyper="Set the value(s) in `v` for hyper-parameter `k`")

---

source

优化器

 Optimizer (params:Union[torch.Tensor,Iterable],
            cbs:Union[Callable,collections.abc.MutableSequence],
            **defaults)

fastai 库的基础优化器类，使用 cbs 更新 params

	类型	详情
params	联合类型	模型参数
cbs	联合类型	Optimizer 步进回调函数
defaults	VAR_KEYWORD

add_docs(Optimizer, 
         zero_grad="Standard PyTorch API: Zero all the grad attributes of the parameters",
         step="Standard PyTorch API: Update the stats and execute the steppers in on all parameters that have a grad",
         state_dict="Return the state of the optimizer in a dictionary",
         load_state_dict="Load the content of `sd`",
         clear_state="Reset the state of the optimizer")

初始化优化器

params 将用于创建优化器的 param_groups。如果它是一个参数集合（或生成器），它将是一个包含所有参数的单个 L。要定义多个参数组，params 应作为 L 的集合（或生成器）传递。

注意

在 PyTorch 中，model.parameters() 返回一个包含所有参数的生成器，您可以直接将其传递给 Optimizer。

opt = Optimizer([1,2,3], noop)
test_eq(opt.param_lists, [[1,2,3]])
opt = Optimizer(range(3), noop)
test_eq(opt.param_lists, [[0,1,2]])
opt = Optimizer([[1,2],[3]], noop)
test_eq(opt.param_lists, [[1,2],[3]])
opt = Optimizer(([o,o+1] for o in range(0,4,2)), noop)
test_eq(opt.param_lists, [[0,1],[2,3]])

cbs 是在应用步进时将组合的一系列函数。例如，您可以将执行 SGD 步进的函数与应用权重衰减的函数组合起来。此外，每个 cb 可以有一个 defaults 属性，其中包含超参数及其默认值。这些在初始化时都会被收集起来，可以通过传递 defaults 关键字参数来覆盖这些默认值。步进器将由 Optimizer.step 调用（这是标准的 PyTorch 名称），梯度可以通过 Optimizer.zero_grad 清除（这也是标准的 PyTorch 名称）。

一旦所有默认值都被提取出来，它们将根据 param_groups 的数量进行复制并存储在 hypers 中。要将不同的超参数应用于不同的组（例如，不同的学习率或某些层不应用权重衰减），您需要在初始化后调整这些值。

def tst_arg(p, lr=0, **kwargs): return p
tst_arg.defaults = dict(lr=1e-2)

def tst_arg2(p, lr2=0, **kwargs): return p
tst_arg2.defaults = dict(lr2=1e-3)

def tst_arg3(p, mom=0, **kwargs): return p
tst_arg3.defaults = dict(mom=0.9)

def tst_arg4(p, **kwargs): return p

opt = Optimizer([1,2,3], [tst_arg,tst_arg2, tst_arg3])
test_eq(opt.hypers, [{'lr2': 1e-3, 'mom': 0.9, 'lr': 1e-2}])
opt = Optimizer([1,2,3], tst_arg, lr=0.1)
test_eq(opt.hypers, [{'lr': 0.1}])
opt = Optimizer([[1,2],[3]], tst_arg)
test_eq(opt.hypers, [{'lr': 1e-2}, {'lr': 1e-2}])
opt = Optimizer([[1,2],[3]], tst_arg, lr=0.1)
test_eq(opt.hypers, [{'lr': 0.1}, {'lr': 0.1}])

对于每个超参数，如果存在多个参数组，您可以传递一个切片或一个集合来设置它们。切片将从其开始到结束被转换为对数均匀分布的集合；如果它只有一个结束值 e，则转换为与参数组数量相同的值集合，其形式为 ...,e/10,e/10,e。

使用元素数量与优化器参数组数量不同的集合设置超参数将引发错误。

opt = Optimizer([[1,2],[3]], tst_arg, lr=[0.1,0.2])
test_eq(opt.hypers, [{'lr': 0.1}, {'lr': 0.2}])
opt = Optimizer([[1,2],[3],[4]], tst_arg, lr=slice(1e-2))
test_eq(opt.hypers, [{'lr': 1e-3}, {'lr': 1e-3}, {'lr': 1e-2}])
opt = Optimizer([[1,2],[3],[4]], tst_arg, lr=slice(1e-4,1e-2))
test_eq(opt.hypers, [{'lr': 1e-4}, {'lr': 1e-3}, {'lr': 1e-2}])
test_eq(opt.param_groups, [{'params': [1,2], 'lr': 1e-4}, {'params': [3], 'lr': 1e-3}, {'params': [4], 'lr': 1e-2}])
test_fail(lambda: Optimizer([[1,2],[3],[4]], tst_arg, lr=np.array([0.1,0.2])))

基本步进器

为了能够给出优化器步进的示例，我们需要一些步进器，如下所示：

---

source

sgd_step

 sgd_step (p, lr, **kwargs)

def tst_param(val, grad=None):
    "Create a tensor with `val` and a gradient of `grad` for testing"
    res = tensor([val]).float()
    res.grad = tensor([val/10 if grad is None else grad]).float()
    return res

p = tst_param(1., 0.1)
sgd_step(p, 1.)
test_eq(p, tensor([0.9]))
test_eq(p.grad, tensor([0.1]))

---

source

weight_decay

 weight_decay (p, lr, wd, do_wd=True, **kwargs)

权重衰减：使用 lr*wd 来衰减 p

p = tst_param(1., 0.1)
weight_decay(p, 1., 0.1)
test_eq(p, tensor([0.9]))
test_eq(p.grad, tensor([0.1]))

---

source

l2_reg

 l2_reg (p, lr, wd, do_wd=True, **kwargs)

L2 正则化：将 wd*p 添加到 p.grad

p = tst_param(1., 0.1)
l2_reg(p, 1., 0.1)
test_eq(p, tensor([1.]))
test_eq(p.grad, tensor([0.2]))

警告

对于基本的 SGD，权重衰减和 L2 正则化是相同的。但对于更复杂的优化器，它们非常不同。

执行步进

---

source

Optimizer.step

 Optimizer.step (closure=None)

此方法将遍历所有参数组，然后遍历所有 grad 不为 None 的参数，并调用 stepper 中的每个函数，将参数 p 以及 hypers 中对应字典中的超参数传递给它。

#test basic step
r = L.range(4)
def tst_params(): return r.map(tst_param)

params = tst_params()
opt = Optimizer(params, sgd_step, lr=0.1)
opt.step()
test_close([p.item() for p in params], r.map(mul(0.99)))

#test two steps
params = tst_params()
opt = Optimizer(params, [weight_decay, sgd_step], lr=0.1, wd=0.1)
opt.step()
test_close([p.item() for p in params], r.map(mul(0.98)))

#test None gradients are ignored
params = tst_params()
opt = Optimizer(params, sgd_step, lr=0.1)
params[-1].grad = None
opt.step()
test_close([p.item() for p in params], [0., 0.99, 1.98, 3.])

#test discriminative lrs
params = tst_params()
opt = Optimizer([params[:2], params[2:]], sgd_step, lr=0.1)
opt.hypers[0]['lr'] = 0.01
opt.step()
test_close([p.item() for p in params], [0., 0.999, 1.98, 2.97])

---

source

Optimizer.zero_grad

 Optimizer.zero_grad ()

params = tst_params()
opt = Optimizer(params, [weight_decay, sgd_step], lr=0.1, wd=0.1)
opt.zero_grad()
[test_eq(p.grad, tensor([0.])) for p in params];

一些 Optimizer 的 cbs 可以是更新与参数关联的状态的函数。该状态随后可以被任何步进器使用。最好的例子是动量计算。

def tst_stat(p, **kwargs): 
    s = kwargs.get('sum', torch.zeros_like(p)) + p.data
    return {'sum': s}
tst_stat.defaults = {'mom': 0.9}

#Test Optimizer init
opt = Optimizer([1,2,3], tst_stat)
test_eq(opt.hypers, [{'mom': 0.9}])
opt = Optimizer([1,2,3], tst_stat, mom=0.99)
test_eq(opt.hypers, [{'mom': 0.99}])

#Test stat
x = torch.randn(4,5)
state = tst_stat(x)
assert 'sum' in state
test_eq(x, state['sum'])
state = tst_stat(x, **state)
test_eq(state['sum'], 2*x)

统计信息

---

source

average_grad

 average_grad (p, mom, dampening=False, grad_avg=None, **kwargs)

使用 mom 跟踪 state 中 p 的平均梯度。

dampening=False 给出 SGD 中动量的经典公式

new_val = old_val * mom + grad

而 dampening=True 使其成为指数移动平均

new_val = old_val * mom + grad * (1-mom)

p = tst_param([1,2,3], [4,5,6])
state = {}
state = average_grad(p, mom=0.9, **state)
test_eq(state['grad_avg'], p.grad)
state = average_grad(p, mom=0.9, **state)
test_eq(state['grad_avg'], p.grad * 1.9)

#Test dampening
state = {}
state = average_grad(p,  mom=0.9, dampening=True, **state)
test_eq(state['grad_avg'], 0.1*p.grad)
state = average_grad(p, mom=0.9, dampening=True, **state)
test_close(state['grad_avg'], (0.1*0.9+0.1)*p.grad)

---

source

average_sqr_grad

 average_sqr_grad (p, sqr_mom, dampening=True, sqr_avg=None, **kwargs)

dampening=False 给出 SGD 中动量的经典公式

new_val = old_val * mom + grad**2

而 dampening=True 使其成为指数移动平均

new_val = old_val * mom + (grad**2) * (1-mom)

p = tst_param([1,2,3], [4,5,6])
state = {}
state = average_sqr_grad(p, sqr_mom=0.99, dampening=False, **state)
test_eq(state['sqr_avg'], p.grad.pow(2))
state = average_sqr_grad(p, sqr_mom=0.99, dampening=False, **state)
test_eq(state['sqr_avg'], p.grad.pow(2) * 1.99)

#Test dampening
state = {}
state = average_sqr_grad(p, sqr_mom=0.99, **state)
test_close(state['sqr_avg'], 0.01*p.grad.pow(2))
state = average_sqr_grad(p, sqr_mom=0.99, **state)
test_close(state['sqr_avg'], (0.01*0.99+0.01)*p.grad.pow(2))

冻结模型部分

---

source

Optimizer.freeze

 Optimizer.freeze ()

---

source

Optimizer.freeze_to

 Optimizer.freeze_to (n:int)

	类型	详情
n	整型	冻结最多 n 层

---

source

Optimizer.unfreeze

 Optimizer.unfreeze ()

#Freezing the first layer
params = [tst_params(), tst_params(), tst_params()]
opt = Optimizer(params, sgd_step, lr=0.1)
opt.freeze_to(1)
req_grad = Self.requires_grad()
test_eq(L(params[0]).map(req_grad), [False]*4)
for i in {1,2}: test_eq(L(params[i]).map(req_grad), [True]*4)
    
#Unfreezing
opt.unfreeze()
for i in range(2): test_eq(L(params[i]).map(req_grad), [True]*4)

#TODO: test warning
# opt.freeze_to(3)

诸如 batchnorm 权重/偏置之类的参数可以标记为始终处于训练模式，只需在它们的状态中设置 force_train=true。

params = [tst_params(), tst_params(), tst_params()]
opt = Optimizer(params, sgd_step, lr=0.1)
for p in L(params[1])[[1,3]]: opt.state[p] = {'force_train': True}
opt.freeze()
test_eq(L(params[0]).map(req_grad), [False]*4)
test_eq(L(params[1]).map(req_grad), [False, True, False, True])
test_eq(L(params[2]).map(req_grad), [True]*4)

序列化

---

source

Optimizer.state_dict

 Optimizer.state_dict ()

---

source

Optimizer.load_state_dict

 Optimizer.load_state_dict (sd:dict)

	类型	详情
sd	字典	包含 hypers 和 state 的状态字典，用于加载到优化器

p = tst_param([1,2,3], [4,5,6])
opt = Optimizer(p, average_grad)
opt.step()
test_eq(opt.state[p]['grad_avg'], tensor([[4., 5., 6.]]))

sd = opt.state_dict()
p1 = tst_param([10,20,30], [40,50,60])
opt = Optimizer(p1, average_grad, mom=0.99)
test_eq(opt.hypers[0]['mom'], 0.99)
test_eq(opt.state, {})

opt.load_state_dict(sd)
test_eq(opt.hypers[0]['mom'], 0.9)
test_eq(opt.state[p1]['grad_avg'], tensor([[4., 5., 6.]]))

---

source

Optimizer.clear_state

 Optimizer.clear_state ()

p = tst_param([1,2,3], [4,5,6])
opt = Optimizer(p, average_grad)
opt.state[p] = {'force_train': True}
opt.step()
test_eq(opt.state[p]['grad_avg'], tensor([[4., 5., 6.]]))

opt.clear_state()
test_eq(opt.state[p], {'force_train': True})

优化器

带动量的 SGD

---

source

momentum_step

 momentum_step (p, lr, grad_avg, **kwargs)

使用 lr 的带动量 SGD 步进

---

source

SGD

 SGD (params:Union[torch.Tensor,Iterable], lr:float|slice, mom:float=0.0,
      wd:numbers.Real=0.0, decouple_wd:bool=True)

一个 SGD Optimizer

	类型	默认值	详情
params	联合类型		模型参数
lr	浮点数 | 切片		默认学习率
mom	浮点数	0.0	梯度移动平均 (β1) 系数
wd	实数	0.0	可选的权重衰减（真权重衰减或 L2）
decouple_wd	布尔型	True	应用真权重衰减或 L2 正则化 (SGD)
返回值	优化器

应用可选的 wd 权重衰减，如果 decouple_wd=True 则作为真权重衰减（直接衰减权重），否则作为 L2 正则化（将衰减添加到梯度）。

#Vanilla SGD
params = tst_params()
opt = SGD(params, lr=0.1)
opt.step()
test_close([p.item() for p in params], [i*0.99 for i in range(4)])
opt.step()
test_close([p.item() for p in params], [i*0.98 for i in range(4)])

#SGD with momentum
params = tst_params()
opt = SGD(params, lr=0.1, mom=0.9)
assert isinstance(opt, Optimizer)
opt.step()
test_close([p.item() for p in params], [i*0.99 for i in range(4)])
opt.step()
test_close([p.item() for p in params], [i*(1 - 0.1 * (0.1 + 0.1*1.9)) for i in range(4)])
for i,p in enumerate(params): test_close(opt.state[p]['grad_avg'].item(), i*0.19)

测试权重衰减，注意即使对于简单的带动量 SGD，L2 正则化与权重衰减也不同。

params = tst_params()
#Weight decay
opt = SGD(params, lr=0.1, mom=0.9, wd=0.1)
opt.step()
test_close([p.item() for p in params], [i*0.98 for i in range(4)])
#L2 reg
opt = SGD(params, lr=0.1, mom=0.9, wd=0.1, decouple_wd=False)
opt.step()
#TODO: fix cause this formula was wrong
#test_close([p.item() for p in params], [i*0.97 for i in range(4)])

RMSProp

---

source

rms_prop_step

 rms_prop_step (p, lr, sqr_avg, eps, grad_avg=None, **kwargs)

使用 lr 的带动量 RMSProp 步进

---

source

RMSProp

 RMSProp (params:Union[torch.Tensor,Iterable], lr:float|slice,
          mom:float=0.0, sqr_mom:float=0.99, eps:float=1e-08,
          wd:numbers.Real=0.0, decouple_wd:bool=True)

一个 RMSProp Optimizer

	类型	默认值	详情
params	联合类型		模型参数
lr	浮点数 | 切片		默认学习率
mom	浮点数	0.0	梯度移动平均 (β1) 系数
sqr_mom	浮点数	0.99	梯度平方移动平均 (β2) 系数
eps	浮点数	1e-08	为数值稳定性添加
wd	实数	0.0	可选的权重衰减（真权重衰减或 L2）
decouple_wd	布尔型	True	应用真权重衰减或 L2 正则化 (RMSProp)
返回值	优化器

RMSProp 由 Geoffrey Hinton 在他的课程中介绍。这里命名为 sqr_mom 的参数在课程中是 alpha。应用可选的 wd 权重衰减，如果 decouple_wd=True 则作为真权重衰减（直接衰减权重），否则作为 L2 正则化（将衰减添加到梯度）。

#Without momentum
params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = RMSProp(params, lr=0.1)
opt.step()
test_close(params[0], tensor([0.,1.,2.]))
opt.step()
step = - 0.1 * 0.1 / (math.sqrt((0.01*0.99+0.01) * 0.1**2) + 1e-8)
test_close(params[0], tensor([step, 1+step, 2+step]))

#With momentum
params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = RMSProp(params, lr=0.1, mom=0.9)
opt.step()
test_close(params[0], tensor([0.,1.,2.]))
opt.step()
step = - 0.1 * (0.1 + 0.9*0.1) / (math.sqrt((0.01*0.99+0.01) * 0.1**2) + 1e-8)
test_close(params[0], tensor([step, 1+step, 2+step]))

Adam

---

source

step_stat

 step_stat (p, step=0, **kwargs)

在 state 中记录 p 已完成的步数

p = tst_param(1,0.1)
state = {}
state = step_stat(p, **state)
test_eq(state['step'], 1)
for _ in range(5): state = step_stat(p, **state)
test_eq(state['step'], 6)

---

source

debias

 debias (mom, damp, step)

---

source

adam_step

 adam_step (p, lr, mom, step, sqr_mom, grad_avg, sqr_avg, eps, **kwargs)

使用 lr 对 p 应用 Adam 步进

---

source

Adam

 Adam (params:Union[torch.Tensor,Iterable], lr:float|slice, mom:float=0.9,
       sqr_mom:float=0.99, eps:float=1e-05, wd:numbers.Real=0.01,
       decouple_wd:bool=True)

一个 Adam/AdamW Optimizer

	类型	默认值	详情
params	联合类型		模型参数
lr	浮点数 | 切片		默认学习率
mom	浮点数	0.9	梯度移动平均 (β1) 系数
sqr_mom	浮点数	0.99	梯度平方移动平均 (β2) 系数
eps	浮点数	1e-05	为数值稳定性添加
wd	实数	0.01	可选的权重衰减（真权重衰减或 L2）
decouple_wd	布尔型	True	应用真权重衰减 (AdamW) 或 L2 正则化 (Adam)
返回值	优化器

Adam 由 Diederik P. Kingma 和 Jimmy Ba 在Adam: A Method for Stochastic Optimization中介绍。为了优化器之间的一致性，我们将论文中的 beta1 和 beta2 重命名为 mom 和 sqr_mom。请注意，我们的默认值也与论文不同（sqr_mom 或 beta2 为 0.99，eps 为 1e-5）。根据我们在各种情况下的实验，这些值似乎更好。

应用可选的 wd 权重衰减，如果 decouple_wd=True 则作为真权重衰减（直接衰减权重），否则作为 L2 正则化（将衰减添加到梯度）。

注意

别忘了 eps 是一个可以更改的超参数。有些模型没有非常高的 eps（例如 0.1）将无法训练（直观地说，eps 越高，我们越接近普通的 SGD）。通常的默认值 1e-8 往往过于极端，因为我们无法获得与 SGD 同样好的结果。

params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = Adam(params, lr=0.1, wd=0)
opt.step()
step = -0.1 * 0.1 / (math.sqrt(0.1**2) + 1e-8)
test_close(params[0], tensor([1+step, 2+step, 3+step]))
opt.step()
test_close(params[0], tensor([1+2*step, 2+2*step, 3+2*step]), eps=1e-3)

RAdam

RAdam（Rectified Adam 的缩写）由 Zhang 等人在On the Variance of the Adaptive Learning Rate and Beyond中提出，旨在轻微修改 Adam 优化器，使其在训练初期更加稳定（因此不需要长时间的热身）。他们估算平方梯度移动平均（传统 Adam 分母中的项）的方差，并在执行更新之前通过该项对该移动平均进行重新缩放。

此版本还集成了SAdam；设置 beta 以启用此功能（定义与论文中相同）。

---

source

radam_step

 radam_step (p, lr, mom, step, sqr_mom, grad_avg, sqr_avg, eps, beta,
             **kwargs)

使用 lr 对 p 应用 RAdam 步进

---

source

RAdam

 RAdam (params:Union[torch.Tensor,Iterable], lr:float|slice,
        mom:float=0.9, sqr_mom:float=0.99, eps:float=1e-05,
        wd:numbers.Real=0.0, beta:float=0.0, decouple_wd:bool=True)

一个 RAdam/RAdamW Optimizer

	类型	默认值	详情
params	联合类型		模型参数
lr	浮点数 | 切片		默认学习率
mom	浮点数	0.9	梯度移动平均 (β1) 系数
sqr_mom	浮点数	0.99	梯度平方移动平均 (β2) 系数
eps	浮点数	1e-05	为数值稳定性添加
wd	实数	0.0	可选的权重衰减（真权重衰减或 L2）
beta	浮点数	0.0	设置为启用 SAdam
decouple_wd	布尔型	True	应用真权重衰减 (RAdamW) 或 L2 正则化 (RAdam)
返回值	优化器

这是 RAdam 中对 Adam 步进进行 500 次迭代后报告的有效修正。我们可以看到它如何从 0 变为 1，模拟了热身的效果。

beta = 0.99
r_inf = 2/(1-beta) - 1
rs = np.array([r_inf - 2*s*beta**s/(1-beta**s) for s in range(5,500)])
v = np.sqrt(((rs-4) * (rs-2) * r_inf)/((r_inf-4)*(r_inf-2)*rs))
plt.plot(v);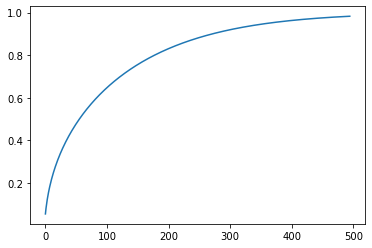

params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = RAdam(params, lr=0.1)
#The r factor is lower than 5 during the first 5 steps so updates use the average of gradients (all the same)
r_inf = 2/(1-0.99) - 1
for i in range(5): 
    r = r_inf - 2*(i+1)*0.99**(i+1)/(1-0.99**(i+1))
    assert r <= 5
    opt.step()
p = tensor([0.95, 1.9, 2.85])
test_close(params[0], p)

#The r factor is greater than 5 for the sixth step so we update with RAdam
r = r_inf - 2*6*0.99**6/(1-0.99**6)
assert r > 5
opt.step()
v = math.sqrt(((r-4) * (r-2) * r_inf)/((r_inf-4)*(r_inf-2)*r))
step = -0.1*0.1*v/(math.sqrt(0.1**2) + 1e-8)
test_close(params[0], p+step)

QHAdam

QHAdam（Quasi-Hyperbolic Adam 的缩写）由 Ma & Yarats 在Quasi-Hyperbolic Momentum and Adam for Deep Learning中提出，作为一种“计算开销小、直观易懂且实现简单”的优化器。额外的代码可以在他们的qhoptim 仓库中找到。QHAdam 基于 QH-Momentum，它引入了即时折扣因子 nu，包含纯 SGD (nu = 0) 和动量 (nu = 1)。QH-Momentum 定义如下，其中 g_t+1 是矩的更新。对 QHM 的解释是动量更新步进和纯 SGD 更新步进的 nu 加权平均。

θ_t+1 ← θ_t − lr * [(1 − nu) · ∇L_t(θ_t) + nu · g_t+1]

QHAdam 采用上面 QHM 背后的概念并将其应用于 Adam，用准双曲项替换 Adam 的两个矩估计器。

论文建议的默认参数是 mom = 0.999, sqr_mom = 0.999, nu_1 = 0.7 和 nu_2 = 1.0。当训练不稳定时，设置 nu_2 < 1 可能通过施加更严格的步长界限来提高稳定性。注意，当 nu_1 = nu_2 = 1.0 时，QHAdam 退化为 Adam。当 nu_1 = 0 且 nu_2 = 1 时，QHAdam 退化为 RMSProp (Hinton et al., 2012)；当 nu_1 = mom 且 nu_2 = 1 时，QHAdam 退化为 NAdam (Dozat, 2016)。

应用可选的 wd 权重衰减，如果 decouple_wd=True 则作为真权重衰减（直接衰减权重），否则作为 L2 正则化（将衰减添加到梯度）。

---

source

qhadam_step

 qhadam_step (p, lr, mom, sqr_mom, sqr_avg, nu_1, nu_2, step, grad_avg,
              eps, **kwargs)

---

source

QHAdam

 QHAdam (params:Union[torch.Tensor,Iterable], lr:float|slice,
         mom:float=0.999, sqr_mom:float=0.999, nu_1:float=0.7,
         nu_2:float=1.0, eps:float=1e-08, wd:numbers.Real=0.0,
         decouple_wd:bool=True)

一个 QHAdam/QHAdamW Optimizer

	类型	默认值	详情
params	联合类型		模型参数
lr	浮点数 | 切片		默认学习率
mom	浮点数	0.999	梯度移动平均 (β1) 系数
sqr_mom	浮点数	0.999	梯度平方移动平均 (β2) 系数
nu_1	浮点数	0.7	QH 即时折扣因子
nu_2	浮点数	1.0	QH 动量折扣因子
eps	浮点数	1e-08	为数值稳定性添加
wd	实数	0.0	可选的权重衰减（真权重衰减或 L2）
decouple_wd	布尔型	True	应用真权重衰减 (QHAdamW) 或 L2 正则化 (QHAdam)
返回值	优化器

params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = QHAdam(params, lr=0.1)
opt.step()
step = -0.1 * (((1-0.7) * 0.1) + (0.7 * 0.1)) / (
     math.sqrt(((1-1.0) * 0.1**2) + (1.0 * 0.1**2)) + 1e-8) 
test_close(params[0], tensor([1+step, 2+step, 3+step]))
opt.step()
test_close(params[0], tensor([1+2*step, 2+2*step, 3+2*step]), eps=1e-3)

LARS/LARC

---

source

larc_layer_lr

 larc_layer_lr (p, lr, trust_coeff, wd, eps, clip=True, **kwargs)

计算应用权重衰减之前的局部学习率

---

source

larc_step

 larc_step (p, local_lr, grad_avg=None, **kwargs)

使用 LARC 对 p 应用 local_lr 步进

---

source

Larc

 Larc (params:Union[torch.Tensor,Iterable], lr:float|slice, mom:float=0.9,
       clip:bool=True, trust_coeff:float=0.02, eps:float=1e-08,
       wd:numbers.Real=0.0, decouple_wd:bool=True)

一个 LARC/LARS Optimizer

	类型	默认值	详情
params	联合类型		模型参数
lr	浮点数 | 切片		默认学习率
mom	浮点数	0.9	梯度移动平均 (β1) 系数
clip	布尔型	True	如果 clip=True 则为 LARC，如果 clip=False 则为 LARS
trust_coeff	浮点数	0.02	用于计算逐层学习率的信任系数
eps	浮点数	1e-08	为数值稳定性添加
wd	实数	0.0	可选的权重衰减（真权重衰减或 L2）
decouple_wd	布尔型	True	应用真权重衰减或 L2 正则化
返回值	优化器

LARS 优化器最初在Large Batch Training of Convolutional Networks中提出，随后在其 LARC 变体中进行了改进（原始 LARS 的 clip=False）。为每个单独的层计算一个具有特定 trust_coefficient 的学习率，然后将其裁剪为始终小于 lr。

应用可选的 wd 权重衰减，如果 decouple_wd=True 则作为真权重衰减（直接衰减权重），否则作为 L2 正则化（将衰减添加到梯度）。

params = [tst_param([1,2,3], [0.1,0.2,0.3]), tst_param([1,2,3], [0.01,0.02,0.03])]
opt = Larc(params, lr=0.1)
opt.step()
#First param local lr is 0.02 < lr so it's not clipped
test_close(opt.state[params[0]]['local_lr'], 0.02)
#Second param local lr is 0.2 > lr so it's clipped
test_eq(opt.state[params[1]]['local_lr'], 0.1)
test_close(params[0], tensor([0.998,1.996,2.994]))
test_close(params[1], tensor([0.999,1.998,2.997]))

params = [tst_param([1,2,3], [0.1,0.2,0.3]), tst_param([1,2,3], [0.01,0.02,0.03])]
opt = Larc(params, lr=0.1, clip=False)
opt.step()
#No clipping
test_close(opt.state[params[0]]['local_lr'], 0.02)
test_close(opt.state[params[1]]['local_lr'], 0.2)
test_close(params[0], tensor([0.998,1.996,2.994]))
test_close(params[1], tensor([0.998,1.996,2.994]))

LAMB

---

source

lamb_step

 lamb_step (p, lr, mom, step, sqr_mom, grad_avg, sqr_avg, eps, **kwargs)

使用 lr 对 p 应用 LAMB 步进

---

source

Lamb

 Lamb (params:Union[torch.Tensor,Iterable], lr:float|slice, mom:float=0.9,
       sqr_mom:float=0.99, eps:float=1e-05, wd:numbers.Real=0.0,
       decouple_wd:bool=True)

一个 LAMB Optimizer

	类型	默认值	详情
params	联合类型		模型参数
lr	浮点数 | 切片		默认学习率
mom	浮点数	0.9	梯度移动平均 (β1) 系数
sqr_mom	浮点数	0.99	梯度平方移动平均 (β2) 系数
eps	浮点数	1e-05	为数值稳定性添加
wd	实数	0.0	可选的权重衰减（真权重衰减或 L2）
decouple_wd	布尔型	True	应用真权重衰减或 L2 正则化
返回值	优化器

LAMB 在Large Batch Optimization for Deep Learning: Training BERT in 76 minutes中提出。直观地说，它是应用于 Adam 的 LARC。与Adam中一样，我们将论文中的 beta1 和 beta2 重命名为 mom 和 sqr_mom。请注意，我们的默认值也与论文不同（sqr_mom 或 beta2 为 0.99，eps 为 1e-5）。根据我们在各种情况下的实验，这些值似乎更好。

应用可选的 wd 权重衰减，如果 decouple_wd=True 则作为真权重衰减（直接衰减权重），否则作为 L2 正则化（将衰减添加到梯度）。

params = tst_param([1,2,3], [0.1,0.2,0.3])
opt = Lamb(params, lr=0.1)
opt.step()
test_close(params[0], tensor([0.7840,1.7840,2.7840]), eps=1e-3)

Lookahead 由 Zhang 等人在Lookahead Optimizer: k steps forward, 1 step back中提出。它可以运行在任何优化器之上，并通过使模型的最终权重成为移动平均来实现。实际上，我们使用内部优化器更新模型，但保留旧权重的副本，并且每 k 步，我们通过对快权重（由内部优化器更新的权重）和慢权重（旧权重的副本）进行移动平均来更改权重。这些慢权重起着稳定性机制的作用。

---

source

Lookahead

 Lookahead (opt:__main__.Optimizer, k:int=6, alpha:float=0.5)

使用 Lookahead 优化器包装 opt

	类型	默认值	详情
opt	优化器		使用 Lookahead 包装的 Optimizer
k	整型	6	执行 Lookahead 步进的频率
alpha	浮点数	0.5	慢权重移动平均系数

params = tst_param([1,2,3], [0.1,0.2,0.3])
p,g = params[0].data.clone(),tensor([0.1,0.2,0.3])
opt = Lookahead(SGD(params, lr=0.1))
for k in range(5): opt.step()
#first 5 steps are normal SGD steps
test_close(params[0], p - 0.5*g)
#Since k=6, sixth step is a moving average of the 6 SGD steps with the initial weight
opt.step()
test_close(params[0], p * 0.5 + (p-0.6*g) * 0.5)

---

source

ranger

 ranger (params:Tensor|Iterable, lr:float|slice, mom:float=0.95,
         wd:Real=0.01, eps:float=1e-06, k:int=6, alpha:float=0.5,
         sqr_mom:float=0.99, beta:float=0.0, decouple_wd:bool=True)

Lookahead 与 RAdam 结合的便捷方法

	类型	默认值	详情
params	Tensor | 可迭代对象		模型参数
lr	浮点数 | 切片		默认学习率
mom	浮点数	0.95	梯度移动平均 (β1) 系数
wd	实数	0.01	可选的权重衰减（真权重衰减或 L2）
eps	浮点数	1e-06	为数值稳定性添加
k	整型	6	执行 Lookahead 步进的频率
alpha	浮点数	0.5	慢权重移动平均系数
sqr_mom	浮点数	0.99	梯度平方移动平均 (β2) 系数
beta	浮点数	0.0	设置为启用 SAdam
decouple_wd	布尔型	True	应用真权重衰减 (RAdamW) 或 L2 正则化 (RAdam)
返回值	Lookahead

OptimWrapper 提供了使用现有由 torch.optim.Optimizer 构造的优化器的简单功能。

---

source

detuplify_pg

 detuplify_pg (d)

---

source

set_item_pg

 set_item_pg (pg, k, v)

---

source

OptimWrapper

 OptimWrapper (params:Union[torch.Tensor,Iterable]=None,
               opt:Union[Callable,torch.optim.optimizer.Optimizer]=None,
               hp_map:dict=None, convert_groups:bool=True, **kwargs)

现有 PyTorch 优化器的包装类

	类型	默认值	详情
params	联合类型	None	模型参数。如果使用已构建的优化器，则无需设置
opt	联合类型	None	一个 torch 优化器构造函数，或一个已构建的优化器
hp_map	字典	None	一个字典，将 PyTorch 优化器键转换为 fastai 的 Optimizer 键。默认为 pytorch_hp_map
convert_groups	布尔型	True	转换来自 splitter 的参数组或将其原样传递给 opt
kwargs	VAR_KEYWORD

要使用现有的 PyTorch 优化器，您可以像这样定义一个优化器函数

opt_func = partial(OptimWrapper, opt=torch.optim.SGD)

或者如果您已经有一个已构建的优化器，则只传入 opt

opt = torch.optim.SGD([tensor([1,2,3])], lr=1e-2)
opt_func = OptimWrapper(opt=opt)

将已构建的优化器传递给 Learner 时，Learner.fit 不会重置优化器，而是会在 reset_opt=True 时或首次调用 Learner.fit 时清除优化器状态。

为了防止 Learner 在首次调用 Learner.fit 时清除优化器状态，请将优化器直接赋值给 Learner.opt

opt = torch.optim.SGD([tensor([1,2,3])], lr=1e-2)
learn = Learner(..., opt_func=None)
learn.opt = OptimWrapper(opt=opt)